Go语言的一些练习题(二)

题目1

随机生成10个整数(1_100的范围)保存到数组，并倒序打印以及求平均值、求最大值和最大值的下标、并查找里面是否有55

思路：

  1. 使用rand
  2. 使用冒泡排序，倒序
  3. 求平均值、最大值为第一个、第一个的下标就是最大值的下标
  4. 使用二分法查找55

自己写的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
package main

import (
	"fmt"
	"math/rand"
)

func ReverseOrder(arr *[10]int) {
	temp := 0 //临时变量用于交换
	for i := 0; i < len(*arr); i++ {
		for j := 0; j < len(*arr) - i - 1; j ++ {
			if (*arr)[j] < (*arr)[j+1] {
				// 交换
				temp = (*arr)[j]
				(*arr)[j] = (*arr)[j+1]
				(*arr)[j+1] = temp
			}
		}
	}
	// 找出最大值和下标
	maxVal := (*arr)[0]
	maxIndex := 0
	for i, val := range *arr {
		if val > maxVal {
			maxVal = val
			maxIndex = i
		}
	}
	fmt.Println("倒序排列后的数组:", *arr)
	fmt.Println("最大值:", maxVal)
    fmt.Println("最大值的下标:", maxIndex)
}

func Average(arr *[10]int) {
	// 遍历数组求平均值
	sum := 0.0 
	for i := 0; i < len(*arr); i++ {
		sum += float64((*arr)[i])
	}
	fmt.Println("平均值为：", sum/float64(len(*arr)))
}

func BinarySearch(arr *[10]int, findval, leftIndex, rightIndex int) {
	//判断leftIndex > rightIndex，则没有找到
	if leftIndex > rightIndex {
		fmt.Println("没有找到目标数字")
		return
	}
	// 先找到中间的下标
	midIndex := (leftIndex + rightIndex) / 2
	if (*arr)[midIndex] > findval {
		// 向左查找
		BinarySearch(arr, findval, leftIndex, midIndex - 1)
	} else if (*arr)[midIndex] < findval {
		// 向右查找
		BinarySearch(arr, findval, midIndex + 1, rightIndex)
	} else {
		fmt.Println("找到下标为：", midIndex)
		return
	}
}
func main() {
	// 随机生成10个1-100的整数
	var nums [10]int
	for i := 0; i < len(nums); i++ {
		nums[i] = rand.Intn(100) + 1
	}
	ReverseOrder(&nums)
	Average(&nums)
	BinarySearch(&nums, 55, 0, len(nums) - 1)
}

代码优化：

  1. 修改 BinarySearch 函数，使其返回找到的目标值下标（若找到），而不是递归调用。移除了不必要的参数 leftIndex 和 rightIndex，并在函数内部初始化。
  2. 在 main() 函数中，调用 BinarySearch 函数查找55，并根据返回值决定是否输出找到的下标。将原来的递归调用替换为直接使用返回值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
package main

import (
	"fmt"
	"math/rand"
)

func ReverseOrder(arr *[10]int) {
	temp := 0 //临时变量用于交换
	for i := 0; i < len(*arr); i++ {
		for j := 0; j < len(*arr) - i - 1; j ++ {
			if (*arr)[j] < (*arr)[j+1] {
				// 交换
				temp = (*arr)[j]
				(*arr)[j] = (*arr)[j+1]
				(*arr)[j+1] = temp
			}
		}
	}
	// 找出最大值和下标
	maxVal := (*arr)[0]
	maxIndex := 0
	for i, val := range *arr {
		if val > maxVal {
			maxVal = val
			maxIndex = i
		}
	}
	fmt.Println("倒序排列后的数组:", *arr)
	fmt.Println("最大值:", maxVal)
    fmt.Println("最大值的下标:", maxIndex)
}

func Average(arr *[10]int) {
	// 遍历数组求平均值
	sum := 0.0
	for _, val := range *arr {
		sum += float64(val)
	}
	fmt.Println("平均值为：", sum/float64(len(*arr)))
}

func BinarySearch(arr *[10]int, findval int) int {
	leftIndex, rightIndex := 0, len(*arr)-1

	// 二分查找
	for leftIndex <= rightIndex {
		midIndex := (leftIndex + rightIndex) / 2
		if (*arr)[midIndex] == findval {
			return midIndex
		} else if (*arr)[midIndex] < findval {
			leftIndex = midIndex + 1
		} else {
			rightIndex = midIndex - 1
		}
	}

	// 没有找到目标值
	fmt.Println("没有找到目标数字")
	return -1
}
func main() {
	// 随机生成10个1-100的整数
	var nums [10]int
	for i := 0; i < len(nums); i++ {
		nums[i] = rand.Intn(100) + 1
	}
	ReverseOrder(&nums)
	Average(&nums)
	index := BinarySearch(&nums, 55)
	if index != -1 {
		fmt.Printf("找到下标为：%d\n", index)
	}
}

题目2

已知有个排序好（升序）的数组，要求插入一个元素，最后打印该数组，顺序依然是升序

思路：

  1. 先输出升序的数组
  2. 将数组变为切片
  3. 然后再随机插入一个数字，进行升序

自己写的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
package main

import (
	"fmt"
	"math/rand"
	"sort"
)

// 升序数组
func ascendingArray(arr *[10]int) {
	temp := 0 //临时变量用于交换
	for i := 0; i < len(*arr); i++ {
		for j := 0; j < len(*arr)-i-1; j++ {
			if (*arr)[j] > (*arr)[j+1] {
				//交换
				temp = (*arr)[j]
				(*arr)[j] = (*arr)[j+1]
				(*arr)[j+1] = temp
			}
		}
	}
	fmt.Println("原本的升序数组:", (*arr))
}

// 将数组转化为切片,并随机增加一个数
func arrayToSlice(arr *[10]int) []int {
	var slice []int
	for i := 0; i < len(*arr); i++ {
		slice = append(slice, (*arr)[i])
	}
	slice = append(slice, randNum())
	return slice
}

// 生成一个100以内的随机数
func randNum() int {
	return rand.Intn(100) + 1
}

// 切片排序
func sliceSort(slice []int) {
	sort.Slice(slice, func(i, j int) bool {
		return slice[i] < slice[j] // 升序排序
	})
	fmt.Println("新的切片排序:", slice)
}

func main() {
	var nums [10]int
	for i := 0; i < len(nums); i++ {
		nums[i] = rand.Intn(100) + 1
	}
	ascendingArray(&nums)
	arrayToSlice(&nums)
	sliceSort(arrayToSlice(&nums))
}

潜在问题和风险

  1. 代码安全性：在arrayToSlice函数中，你对原始数组进行了操作，并返回了一个新的切片。这里没有直接的问题，但是值得注意的是，如果对切片进行了修改，而原始数组没有被预期地更新，这可能会导致一些不容易发现的bug。需要确保在文档中明确这种行为，或者考虑使用不可变对象。
  2. 边界条件：在ascendingArray函数中，你使用了嵌套的for循环进行冒泡排序，但是没有对数组为空或者只有一个元素的情况进行特殊处理。尽管在这种情况下代码仍然有效，但是添加对这些边界条件的检查可以让代码更加健壮。
  3. 异常处理：Go语言中处理错误的方式与许多其他语言不同，需要显式地进行错误检查。虽然在这段代码中没有显式的错误处理需求，但在涉及到随机数生成、排序等可能失败的操作时，应考虑如何优雅地处理潜在的异常情况。

优化方向

  1. 性能效率：
  • 在ascendingArray函数中，冒泡排序的效率在大型数据集上可能较差。考虑对于较大数组使用更高效的排序算法，如快速排序、归并排序等。
  • 当arrayToSlice函数中的数组已知大小为10时，可以预先为切片分配足够的空间，这样append操作将更加高效。即使用slice = make([]int, 0, len(*arr)+1)初始化切片。
  1. 可维护性：
  • 考虑将随机数生成的功能抽象到一个独立的函数中，这样可以提高代码的可读性和可维护性。你已经做到了这一点，这是一个好习惯。
  • 函数命名应清晰表达其功能。例如，ascendingArray实际上是在对数组进行排序，而不是创建一个升序数组。建议更改为sortArrayAscending或其他更能准确描述功能的名称。
  • 注释非常重要，但应确保其准确且有用。例如，在ascendingArray函数中，你对交换过程进行了注释，这是好的。不过，对整个函数的功能和算法的简短说明也会很有帮助。
  1. 代码整洁：
  • 在main函数中，你初始化了一个[10]int类型的数组并填充了随机数，然后将其传递给不同的函数进行操作。这个过程很清晰，但是将初始化和填充数组的代码封装到一个独立的函数中，可以提高代码的可读性和重用性。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
package main

import (
    "fmt"
    "math/rand"
    "sort"
)

// 升序数组
func sortArrayAscending(arr *[10]int) {
    // 特殊处理:数组为空或只有一个元素时,无需排序,直接返回
    if len(*arr) <= 1 {
        fmt.Printf("数组长度小于等于1，无需排序: %v\n", (*arr))
        return
    }

    temp := 0 //临时变量用于交换
    for i := 0; i < len(*arr); i++ {
        for j := 0; j < len(*arr)-i-1; j++ {
            if (*arr)[j] > (*arr)[j+1] {
                //交换
                temp = (*arr)[j]
                (*arr)[j] = (*arr)[j+1]
                (*arr)[j+1] = temp
            }
        }
    }
    fmt.Println("原本的升序数组:", (*arr))
}

// 将数组转化为切片,并随机增加一个数
func arrayToSlice(arr *[10]int) []int {
    // 预先分配足够的空间
    slice := make([]int, 0, len(*arr)+1)
    for i := 0; i < len(*arr); i++ {
        slice = append(slice, (*arr)[i])
    }
    slice = append(slice, randNum())
    return slice
}

// 生成一个100以内的随机数
func randNum() int {
    return rand.Intn(100) + 1
}

// 切片排序
func sliceSort(slice []int) {
    sort.Slice(slice, func(i, j int) bool {
        return slice[i] < slice[j] // 升序排序
    })
    fmt.Println("新的切片排序:", slice)
}

// 初始化并填充一个长度为10的随机数数组
func initRandomArray() [10]int {
    var nums [10]int
    for i := 0; i < len(nums); i++ {
        nums[i] = rand.Intn(100) + 1
    }
    return nums
}

func main() {
    nums := initRandomArray()
    sortArrayAscending(&nums)
    slice := arrayToSlice(&nums)
    sliceSort(slice)
}

题目3

定义一个3行4列的二维数组，逐个从键盘输入值，编写程序将四周的数据清0

原始的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
package main

import (
	"fmt"
)

func main() {
	// 定义一个3行4列的二维数组
	var matrix [3][4]int

	// 从键盘读取12个数字填充到二维数组中
	fmt.Println("请输入12个数字填充到3x4的二维数组中:")
	for i := 0; i < 3; i++ {
		for j := 0; j < 4; j++ {
			fmt.Printf("请输入第%d行第%d列的值: ", i+1, j+1)
			fmt.Scan(&matrix[i][j])
		}
	}

	// 打印原始数组
	fmt.Println("\n原始数组:")
	displayMatrix(matrix)

	// 清除四周的数据（即第一行、最后一行、第一列、最后一列）
	for i := 0; i < 3; i++ {
		matrix[i][0], matrix[i][3] = 0, 0 // 清空第一列和最后一列
	}
	matrix[0], matrix[2] = [4]int{0, 0, 0, 0}, [4]int{0, 0, 0, 0} // 清空第一行和最后一行

	// 打印修改后的数组
	fmt.Println("\n清除四周数据后的数组:")
	displayMatrix(matrix)
}

// displayMatrix 打印二维数组
func displayMatrix(matrix [3][4]int) {
	for _, row := range matrix {
		for _, val := range row {
			fmt.Printf("%d\t", val)
		}
		fmt.Println()
	}
}

潜在问题

  1. 异常处理：当前代码缺乏对用户输入的异常处理。例如，如果用户输入的不是数字，fmt.Scan()将会失败，但程序不会对此做出任何反应或处理。考虑增加错误处理逻辑，确保程序的健壮性。
  2. 输入校验：程序没有校验用户输入的数字是否在合理的范围内。对于本例来说，虽然范围没有明确限制，但如果程序逻辑更复杂，可能需要考虑输入值的合法性（例如，是否为负数等）。
  3. 边界条件处理：在清除数组四周元素的逻辑中，直接将元素赋值为0。这种方式在处理具有特定边界条件要求的数据时可能会不够安全，尤其是在其他上下文中使用该数组时。

优化方向

  1. 代码重构：清除数组四周元素的逻辑略显冗余，可以考虑封装成一个单独的函数以提高代码的可读性和可维护性。例如，可以创建一个函数来处理特定行列的清零操作。
  2. 性能考虑：虽然对于一个3x4的数组来说性能不是问题，但如果处理更大的数组，可以考虑优化数据结构或算法，以减少不必要的操作，比如在清除四周元素时，避免对已清零的元素重复操作。
  3. 输入方式优化：当前通过嵌套循环和多次调用fmt.Scan()来读取输入，这种方式虽然简单但不够高效。考虑使用bufio.Scanner等工具来改善输入效率和用户体验。
  4. 增强交互性：对于需要从用户处获取输入的程序，考虑增加更友好的交互元素，比如输入提示、输入验证消息等，以提升程序的易用性。
  5. 使用更现代的Go特性：Go语言在不断发展，新的语言特性可能会提供更简洁、高效的解决方案。比如使用fmt.Printf(“%d\t”, matrix[i][j])直接在displayMatrix函数中打印矩阵，减少中间变量的使用。

优化后的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
package main

import (
	"bufio"
	"fmt"
	"os"
	"unicode"
)

func main() {
	// 定义一个3行4列的二维数组
	var matrix [3][4]int

	// 从键盘读取12个数字填充到二维数组中
	fmt.Println("请输入12个数字填充到3x4的二维数组中:")
	scanner := bufio.NewScanner(os.Stdin)
	for i := 0; i < 3; i++ {
		for j := 0; j < 4; j++ {
			fmt.Printf("请输入第%d行第%d列的值: ", i+1, j+1)
			if scanner.Scan() {
				if unicode.IsDigit(rune(scanner.Text()[0])) {
					_, err := fmt.Sscanf(scanner.Text(), "%d", &matrix[i][j])
					if err != nil {
						fmt.Println("输入错误，请确保输入一个整数。")
						i--
						continue
					}
				} else {
					fmt.Println("输入错误，请确保输入一个整数。")
					i--
					continue
				}
			} else {
				fmt.Println("读取输入失败。")
				return
			}
		}
	}

	// 打印原始数组
	fmt.Println("\n原始数组:")
	displayMatrix(matrix)

	// 清除四周的数据
	zeroOutSides(&matrix)

	// 打印修改后的数组
	fmt.Println("\n清除四周数据后的数组:")
	displayMatrix(matrix)
}

// displayMatrix 打印二维数组
func displayMatrix(matrix [3][4]int) {
	for _, row := range matrix {
		for _, val := range row {
			fmt.Printf("%d\t", val)
		}
		fmt.Println()
	}
}

// zeroOutSides 清除二维数组的四周元素
func zeroOutSides(matrix *[3][4]int) {
	// Clear first and last columns
	for i := 0; i < 3; i++ {
		matrix[i][0] = 0
		matrix[i][3] = 0
	}

	// Clear first and last rows
	for j := 0; j < 4; j++ {
		matrix[0][j] = 0
		matrix[2][j] = 0
	}
}

题目4

定义一个4行4列的二维数组，逐个从键盘输入值，然后将第1行和第4行的数据进行交换，将第2行和第3行的数据进行交换

提示：可以尝试使用地址交换

最初自己写的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
package main

import (
	"bufio"
	"fmt"
	"os"
	"unicode"
)

func main() {
	// 定义一个4行4列的二维数组
	var matrix [4][4]int

	// 从键盘读取12个数字填充到二维数组中
	fmt.Println("请输入12个数字填充到4x4的二维数组中:")
	scanner := bufio.NewScanner(os.Stdin)
	for i := 0; i < 4; i++ {
		for j := 0; j < 4; j++ {
			fmt.Printf("请输入第%d行第%d列的值: ", i+1, j+1)
			if scanner.Scan() {
				if unicode.IsDigit(rune(scanner.Text()[0])) {
					_, err := fmt.Sscanf(scanner.Text(), "%d", &matrix[i][j])
					if err != nil {
						fmt.Println("输入错误，请确保输入一个整数。")
						i--
						continue
					}
				} else {
					fmt.Println("输入错误，请确保输入一个整数。")
					i--
					continue
				}
			} else {
				fmt.Println("读取输入失败。")
				return
			}
		}
	}

	// 打印原始数组
	fmt.Println("\n原始数组:")
	displayMatrix(matrix)

	// 交换
	swapRows(&matrix, 0, 3)
	swapRows(&matrix, 1, 2)

	fmt.Println("\n交换后数组:")
	displayMatrix(matrix)
}

// displayMatrix 打印二维数组
func displayMatrix(matrix [4][4]int) {
	for _, row := range matrix {
		for _, val := range row {
			fmt.Printf("%d\t", val)
		}
		fmt.Println()
	}
}

// 交换两行的函数
// 使用指针的方法
func swapRows(matrix *[4][4]int, i, j int) {
	//这两行代码分别将矩阵中索引为i和j的两行存储到局部变量oldRowI和oldRowJ中。
	//由于matrix是数组指针，所以需要使用(*matrix)来访问其元素。
	oldRowI := (*matrix)[i]
	oldRowJ := (*matrix)[j]
	(*matrix)[i] = oldRowJ
	(*matrix)[j] = oldRowI
}

潜在问题和风险

  1. 输入校验不够严格：虽然代码对输入进行了是否为数字的判断，但并未校验输入的整数是否在合理的范围内（例如，负数或超出数组索引范围的值）。这可能会导致逻辑错误或运行时panic。
  2. 错误处理不够优雅：当输入格式错误或读取失败时，程序会直接通过fmt.Println输出错误信息并进行一些逻辑处理（如i–），这样的处理方式较为简单，不利于构建更加健壮和用户友好的程序。
  3. 边界条件处理存在潜在风险：在处理输入错误时通过i–来重试当前循环，这可能会导致死循环或逻辑错误，尤其是当输入一直错误时。

优化建议

  1. 增强输入校验：除了检查输入字符是否为数字外，还应该检查扫描后的整数是否在预期的范围内（例如，0到100，或者更具体的范围，根据实际需求确定）。
  2. 改进错误处理：考虑使用更结构化的错误处理方式，例如定义错误类型或使用错误返回值来通知上层调用者发生了什么错误，而不是直接在底层输出错误信息。
  3. *避免使用***i–**进行错误处理：当输入错误时，应该考虑更安全的处理方式，比如使用一个额外的循环来专门处理输入校验失败的情况，避免影响主逻辑的索引计数。
  4. 代码可读性优化：虽然代码逻辑清晰，但在一些地方加入注释（比如swapRows函数的工作原理）可以进一步提高代码的可读性。
  5. 性能考虑：虽然这段程序的性能瓶颈不明显，但在处理大量数据或更复杂的逻辑时，需要注意循环、函数调用等可能的性能开销，考虑是否有必要优化这些方面。
  6. 异常处理：scanner.Scan()可能因为多种原因失败，除了打印错误信息外，考虑是否有更恰当的异常处理或恢复策略，以确保程序的健壮性。

调整后的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
package main

import (
    "bufio"
    "fmt"
    "os"
    "unicode"
)

func main() {
    // 定义一个4行4列的二维数组
    var matrix [4][4]int

    // 从键盘读取12个数字填充到二维数组中
    fmt.Println("请输入12个数字填充到4x4的二维数组中:")
    scanner := bufio.NewScanner(os.Stdin)
    for i := 0; i < 4; i++ {
        for j := 0; j < 4; j++ {
            var validInput bool
            for !validInput {
                fmt.Printf("请输入第%d行第%d列的值: ", i+1, j+1)
                if scanner.Scan() {
                    input := scanner.Text()
                    if unicode.IsDigit(rune(input[0])) {
                        var num int
                        _, err := fmt.Sscanf(input, "%d", &num)
                        if err == nil && num >= 0 && num <= 100 {
                            matrix[i][j] = num
                            validInput = true
                        } else {
                            fmt.Println("输入错误，请确保输入一个0到100之间的整数。")
                        }
                    } else {
                        fmt.Println("输入错误，请确保输入一个整数。")
                    }
                } else {
                    fmt.Println("读取输入失败。")
                    return
                }
            }
        }
    }

    // 打印原始数组
    fmt.Println("\n原始数组:")
    displayMatrix(matrix)

    // 交换
    swapRows(&matrix, 0, 3)
    swapRows(&matrix, 1, 2)

    fmt.Println("\n交换后数组:")
    displayMatrix(matrix)
}

// displayMatrix 打印二维数组
func displayMatrix(matrix [4][4]int) {
    for _, row := range matrix {
        for _, val := range row {
            fmt.Printf("%d\t", val)
        }
        fmt.Println()
    }
}

// 交换两行的函数
// 使用指针的方法
func swapRows(matrix *[4][4]int, i, j int) {
    //这两行代码分别将矩阵中索引为i和j的两行存储到局部变量oldRowI和oldRowJ中。
    //由于matrix是数组指针，所以需要使用(*matrix)来访问其元素。
    oldRowI := (*matrix)[i]
    oldRowJ := (*matrix)[j]
    (*matrix)[i] = oldRowJ
    (*matrix)[j] = oldRowI
}

题目5

保存10以内的奇数到数组，并倒序打印

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
package main

import "fmt"

func main() {
	// 保存10以内的奇数到数组
	var arr [5]int
	i := 0
	for num := 1; num <= 10; num++ {
		if num%2 == 1 {
			arr[i] = num
			i++
		}
	}

	// 倒序打印数组
	for j := len(arr) - 1; j >= 0; j-- {
		fmt.Printf("%d ", arr[j])
	}
	fmt.Println()
}

题目6

试写出实现查找的核心代码，比如已知数组 arr[10]string; 里面保存了十个元素，现要查找”AA”在其中是否存在，打印提示，如果有多个”AA”，也要找到对应的下标。

思路：

这里二分查找无法使用，因为二分查找仅能查找数组中唯一元素

需要使用顺序查找

自己写的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
package main

import "fmt"

func main() {
	// 1.假设数组中有10个元素
	var demo [10]string = [10]string{"1", "2", "CC", "4", "AA", "6", "BB", "AA", "QA", "10"}
	var key string = ""
	fmt.Println("请输入要查找的元素：")
	fmt.Scanln(&key)
	// 2.顺序查找
	index := -1
	// 3. 创建空的切片,用于存放下标的位置
	var time []int = make([]int, 0)
	for i := 0; i < len(demo); i++ {
		if demo[i] == key {
			index = i
			time = append(time, i)
		}
	}
	if index != -1 {
		fmt.Println("找到元素：", demo[index])
		for i := 0; i < len(time); i++ {
			fmt.Println("AA存在的下标为:", time[i])
		}
	} else {
		fmt.Println("未找到元素")
	}
}

潜在问题

  1. 变量命名：变量命名应尽量清晰和具有描述性。例如，demo可以改为data或dataSource，以更明确其作为数据源的角色。time作为存储下标的切片，命名容易引起误解，建议改为indices或foundIndices等。
  2. 硬编码：数组长度和初始值被硬编码在程序中，这限制了代码的灵活性和可重用性。建议通过函数参数等方式增加代码的通用性。
  3. 异常处理和输入验证：程序中未对用户输入进行验证。例如，如果用户输入为空字符串，程序将打印出未找到元素的消息，这可能不是预期的行为。建议增加输入有效性检查。
  4. 性能效率：虽然顺序查找在小数据集上表现良好，但对于更大的数据集，其效率可能较低。如果数据集较大或查找操作频繁，可能需要考虑使用更高效的算法，如二分查找或使用哈希表等数据结构。

优化方向

  1. 代码结构：可以将查找逻辑封装成一个独立的函数，这样做不仅增加了代码的可读性，也便于单元测试和复用。
  2. 性能优化：如果数据集允许，考虑使用更高效的数据结构。例如，如果需要频繁地进行查找操作，可以将数据存储在map中，这样可以将查找时间复杂度降低到O(1)。
  3. 输入处理：使用bufio.Scanner等工具对用户输入进行更有效的处理，同时增加输入验证以提高程序的健壮性。
  4. 可维护性：通过添加注释和文档，解释函数的用途、参数和返回值等，可以大大提高代码的可读性和可维护性。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
package main

import (
	"bufio"
	"fmt"
	"os"
)

// 将查找的逻辑封装成一个独立的函数
func findIndices(data [10]string, key string) []int {
	var indices []int
	for i, value := range data {
		if value == key {
			indices = append(indices, i)
		}
	}
	return indices
}
func main() {
	// 1.假设数组中有10个元素
	dataSource := [10]string{"1", "2", "CC", "4", "AA", "6", "BB", "AA", "QA", "10"}

	fmt.Println("请输入要查找的元素：")
	scanner := bufio.NewScanner(os.Stdin)
	if !scanner.Scan() {
		fmt.Println("无法读取输入,请确保正确输入.")
		return
	}
	searchKey := scanner.Text()
	if scanner.Text() == "" {
		fmt.Println("输入不能为空,请重新输入.")
		return
	}
	indices := findIndices(dataSource, searchKey)
	if len(indices) > 0 {
		fmt.Println("找到元素: ", searchKey)
		//通过使用范围循环来遍历和打印找到下标
		for _, i := range indices {
			fmt.Printf("下标为: %d\n", i)
		}
	} else {
		fmt.Println("未找到元素: ", searchKey)
	}
}

效果如下：

题目6

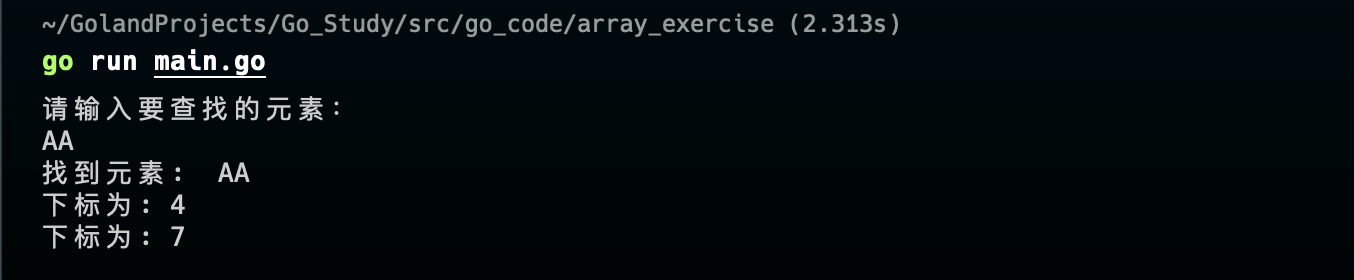
题目7

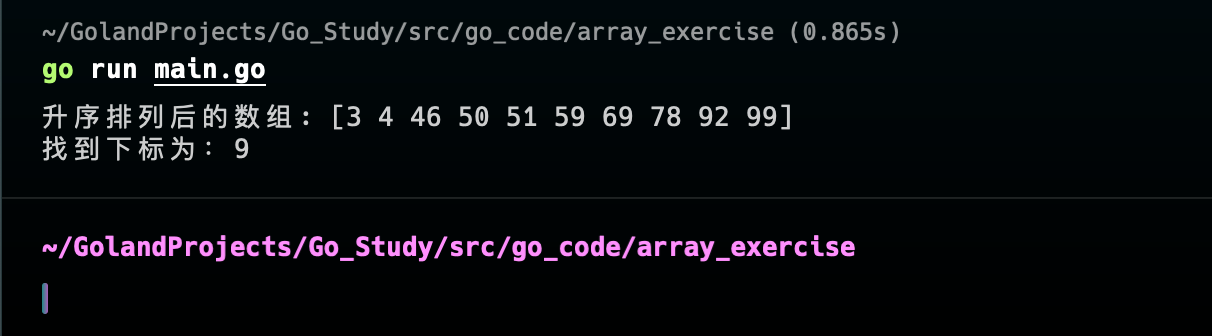
随机生成10个整数(1-100之间)，使用冒泡排序法进行排序，然后使用二分查找法，查找是否有90这个数，并显示下标，如果没有则提示“找不到该数”

这题直接在第一题的基础上调整即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
package main

import (
	"fmt"
	"math/rand"
)

func AscendingArray(arr *[10]int) {
	temp := 0 //临时变量用于交换
	for i := 0; i < len(*arr); i++ {
		for j := 0; j < len(*arr)-i-1; j++ {
			if (*arr)[j] > (*arr)[j+1] {
				temp = (*arr)[j]
				(*arr)[j] = (*arr)[j+1]
				(*arr)[j+1] = temp
			}
		}
	}
	fmt.Println("升序排列后的数组:", (*arr))
}

// 生成100以内的随机数
func randNum() int {
	return rand.Intn(100) + 1
}

func BinarySearch(arr *[10]int, findval int) int {
	leftIndex, rightIndex := 0, len(*arr)-1

	// 二分查找
	for leftIndex <= rightIndex {
		midIndex := (leftIndex + rightIndex) / 2
		if (*arr)[midIndex] == findval {
			return midIndex
		} else if (*arr)[midIndex] < findval {
			leftIndex = midIndex + 1
		} else {
			rightIndex = midIndex - 1
		}
	}

	// 没有找到目标值
	fmt.Println("没有找到目标数字")
	return -1
}

func main() {
	var arr [10]int
	for i := 0; i < len(arr); i++ {
		arr[i] = randNum()
	}
	AscendingArray(&arr)
	index := BinarySearch(&arr, 99)
	if index != -1 {
		fmt.Printf("找到下标为：%d\n", index)
	}
}

题目7

题目8

编写一个函数，可以接收一个数组，该数组有10个数，请找出最大的数和最小的数和对应的数组下标是多少？

自己写的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
package main

import (
	"fmt"
	"math/rand"
)

func findMaxAndIndex(arr []int) (max, index int) {
	if len(arr) == 0 {
		panic("数组为空")
	}
	max = arr[0]
	index = 0
	for i, v := range arr {
		if v > max {
			max = v
			index = i
		}
	}
	return max, index
}

func findMinAndIndex(arr []int) (min, index int) {
	if len(arr) == 0 {
		panic("数组为空")
	}
	min = arr[0]
	index = 0
	for i, v := range arr {
		if v < min {
			min = v
			index = i
		}
	}
	return min, index
}

func randNum() int {
	return rand.Intn(100) + 1
}

func main() {
	var nums [10]int
	for i := 0; i < 10; i++ {
		nums[i] = randNum()
	}
	max, maxIndex := findMaxAndIndex(nums[:])
	min, minIndex := findMinAndIndex(nums[:])
	fmt.Println("切片为:", nums)
	fmt.Println("最大的数为", max)
	fmt.Println("最小的数为", min)
	fmt.Println("最大数的索引为", maxIndex)
	fmt.Println("最小数的索引为", minIndex)
}

潜在优化建议：

  • 合并查找最大值和最小值的函数：虽然当前实现将查找最大值和最小值的逻辑分离为两个函数，但考虑到两者代码结构相似且处理的是同一数组，可以考虑合并为一个函数以减少重复代码。这样不仅提高了代码复用性，也简化了函数调用。
  • 错误处理：在 findMaxAndIndex 和 findMinAndIndex 函数中，您对空数组进行了检查并抛出 panic。然而，由于本例中数组长度固定为10（在 main 函数中初始化），因此实际上不会出现空数组的情况。若考虑代码的通用性，可以保留此错误处理；否则，可以移除以简化代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
package main

import (
	"fmt"
	"math/rand"
)

// findMinMaxAndIndices 合并查找最大值和最小值及其索引的逻辑
func findMinMaxAndIndices(arr []int) (max, min int, maxIndex, minIndex int) {
	if len(arr) == 0 {
		panic("数组为空")
	}
	max = arr[0]
	min = arr[0]
	maxIndex = 0
	minIndex = 0
	for i, v := range arr {
		if v > max {
			max = v
			maxIndex = i
		} else if v < min {
			min = v
			minIndex = i
		}
	}
	return max, min, maxIndex, minIndex
}

func randNum() int {
	return rand.Intn(100) + 1
}

func main() {
	var nums [10]int
	for i := 0; i < 10; i++ {
		nums[i] = randNum()
	}
	max, min, maxIndex, minIndex := findMinMaxAndIndices(nums[:])
	fmt.Println("切片为:", nums)
	fmt.Println("最大的数为", max)
	fmt.Println("最小的数为", min)
	fmt.Println("最大数的索引为", maxIndex)
	fmt.Println("最小数的索引为", minIndex)
}

题目9

定义一个数组，并给出8个整数，求该数组中大于平均值的数的个数，和小于平均值的数的个数。

自己写的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
package main

import (
	"errors"
	"fmt"
	"math/rand"
)

// 求平均值的函数
func average(arr []int) (float64, error) {
	if len(arr) == 0 {
		return 0, errors.New("数组不能为空")
	}
	var sum int = 0
	for _, num := range arr {
		sum += num
	}
	return float64(sum) / float64(len(arr)), nil
}

func randNum() int {
	return rand.Intn(100) + 1
}

// 与平均数比较大小
func compare(arr []int) {
	avg, err := average(arr)
	if err != nil {
		fmt.Println("计算平均值时出错", err)
		return
	}
	fmt.Println("数组的平均值为:", avg)
	var lowcount []int
	var highcount []int
	for i := 0; i < len(arr); i++ {
		if arr[i] > int(avg) {
			highcount = append(highcount, arr[i])
		} else if arr[i] < int(avg) {
			lowcount = append(lowcount, arr[i])
		}
	}
	fmt.Println("大于平均数的值为:", highcount[:], "共", len(highcount), "个")
	fmt.Println("小于平均数的值为:", lowcount[:], "共", len(lowcount), "个")
}
func main() {
	var nums [8]int
	for i := 0; i < 8; i++ {
		nums[i] = randNum()
	}
	fmt.Println("数组为", nums)
	compare(nums[:])
}

优化建议：

  1. 使用常量替代硬编码的数组长度： 已在代码中实现，定义了常量 arrayLength 表示数组长度。
  2. 输出大于和小于平均值的具体元素值： 已在 compare() 函数中实现，通过分别创建切片 greaterValues 和 lowerValues 存储对应元素值，并在循环中添加元素。最后，使用 fmt.Printf() 输出具体元素值及其个数。
  3. 对数组进行排序以方便输出有序元素值： 在 compare() 函数开始处，使用 sort.Ints() 对数组进行升序排序。这样，遍历数组时可以同时输出有序的大于和小于平均值的元素值。

优化后的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
package main

import (
	"errors"
	"fmt"
	"math/rand"
	"sort"
)

// 求平均值的函数
func average(arr []int) (float64, error) {
	if len(arr) == 0 {
		return 0, errors.New("数组不能为空")
	}
	var sum int = 0
	for _, num := range arr {
		sum += num
	}
	return float64(sum) / float64(len(arr)), nil
}

func randNum() int {
	return rand.Intn(100) + 1
}

// 与平均数比较大小,并输入具体元素值
func compare(arr []int) {
	avg, err := average(arr)
	if err != nil {
		fmt.Println("计算平均值时出错", err)
		return
	}
	fmt.Println("数组的平均值为:", avg)

	// 排序数组,便于后续遍历同时输出元素值
	sort.Ints(arr)
	var greaterCount, lowerCount int
	var greaterValues, lowerValues []int
	for _, num := range arr {
		if num > int(avg) {
			greaterCount++
			greaterValues = append(greaterValues, num)
		} else if num < int(avg) {
			lowerCount++
			lowerValues = append(lowerValues, num)
		}
	}
	fmt.Printf("大于平均数的元素值有: %v，共 %d 个\n", greaterValues, greaterCount)
	fmt.Printf("小于平均数的元素值有: %v，共 %d 个\n", lowerValues, lowerCount)
}
func main() {
	var nums [8]int
	for i := 0; i < 8; i++ {
		nums[i] = randNum()
	}
	fmt.Println("数组为", nums)
	compare(nums[:])
}

题目10

跳水比赛，8个评委打分。运动员的成绩是8个成绩取掉一个最高分，去掉一个最低分，剩下的6个分数的平均分就是最后得分。使用一维数组实现如下功能：

(1）请把打最高分的评委和最低分的评委找出来。

(2）找出最佳评委和最差评委。最佳评委就是打分和最后得分最接近的评委。最差评委就是打分和最后得分相差最大的。如果最差和最佳存在多个，都需要打印出来。

思路

  1. 在键盘输入打分，最高分为10分，然后输入全部分数
  2. 使用函数找出最小和最大的元素，删掉，并算出平均分为最终得分
  3. 然后再通过每个元素与最终得分比较，差值最小的数的下标为最佳评委，最大的下标为最差评委

自己写的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
package main

import (
	"bufio"
	"errors"
	"fmt"
	"math"
	"os"
	"strconv"
	"strings"
)

// FindMinMaxIndex 函数返回给定浮点数切片中的最小值、最大值及其索引。
// 如果输入切片为空，将返回错误。
func FindMinMaxIndex(arr []float64) (min, max float64, minIndices []int, maxIndices []int, err error) {
	if len(arr) == 0 {
		return 0, 0, nil, nil, errors.New("输入切片不能为空")
	}

	min = arr[0]
	max = arr[0]

	for i, v := range arr {
		if v < min {
			min = v
			minIndices = []int{i}
		} else if v == min {
			// 处理相等的情况，将索引添加到 minIndices
			minIndices = append(minIndices, i)
		}
		if v > max {
			max = v
			maxIndices = []int{i}
		} else if v == max {
			// 处理相等的情况，将索引添加到 maxIndices
			maxIndices = append(maxIndices, i)
		}
	}

	return min, max, minIndices, maxIndices, nil
}

// 去掉最低分和最高分,算出平均分
func Average(arr []float64) (avg float64, newArr []float64) {
	sum := 0.0
	// 定义切片
	min, max, minIndices, maxIndices, _ := FindMinMaxIndex(arr)
	for _, v := range arr {
		if v != min && v != max {
			sum += v
			newArr = append(newArr, v)
		}
	}
	fmt.Printf("最低分的评委是:%v,最高分的评委是:%v\n", minIndices, maxIndices)
	fmt.Printf("去掉最低分%v和最高分%v后的分数情况:\n%v\n", min, max, newArr)
	avg = sum / float64(len(newArr))
	fmt.Printf("最终得分(即平均分)为:\n%.2f", avg)
	return avg, newArr
}

// 对得分情况取差值
func findIndices(avg float64, arr []float64) {
	if len(arr) == 0 {
		panic("打分错误")
	}
	// 对得分情况取差值
	for i := 0; i < len(arr); i++ {
		arr[i] = arr[i] - avg
	}
	// 对数组newArr中的每个元素取绝对值
	for i := range arr {
		arr[i] = math.Abs(arr[i])
	}
	fmt.Printf("\n每一个分数与平均值的差值:\n%.2f\n", arr)
	min, max, minIndex, maxIndex, err := FindMinMaxIndex(arr)
	if err != nil {
		fmt.Println(err)
	} else {
		fmt.Printf("与最终得分差距最大的是:%.2f\n", max)
		fmt.Printf("与最终得分差距最小的是:%.2f\n", min)
		fmt.Printf("最差评委的下标为:%d\n", maxIndex)
		fmt.Printf("最佳评委的下标为:%d\n", minIndex)
	}
}

func main() {
	// arr := []float64{7, 9.1, 8.9, 9, 9, 6, 7, 10, 9.8, 8.9}
	reader := bufio.NewReader(os.Stdin)
	numbers := make([]float64, 0, 10)
	scoreCount := 0
	fmt.Println("输入评委分数，每行一个。")
	for scoreCount < 10 {
		fmt.Print("请输入分数:")
		input, err := reader.ReadString('\n')
		if err != nil {
			fmt.Println("读取输入时发生错误:", err)
			break
		}
		input = strings.TrimSpace(input)
		if num, err := strconv.ParseFloat(input, 64); err == nil && num >= 0 && num <= 10 {
			numbers = append(numbers, num)
			scoreCount++
			continue // 正确输入，继续请求下一个分数
		} else {
			fmt.Println("分数必须在0到10之间，请重新输入。")
		}
	}
	if len(numbers) > 0 {
		fmt.Printf("评委打分为:\n%v\n", numbers)
		avg, newArr := Average(numbers)
		findIndices(avg, newArr)
	} else {
		fmt.Println("评委未打分")
	}
}

输出结果

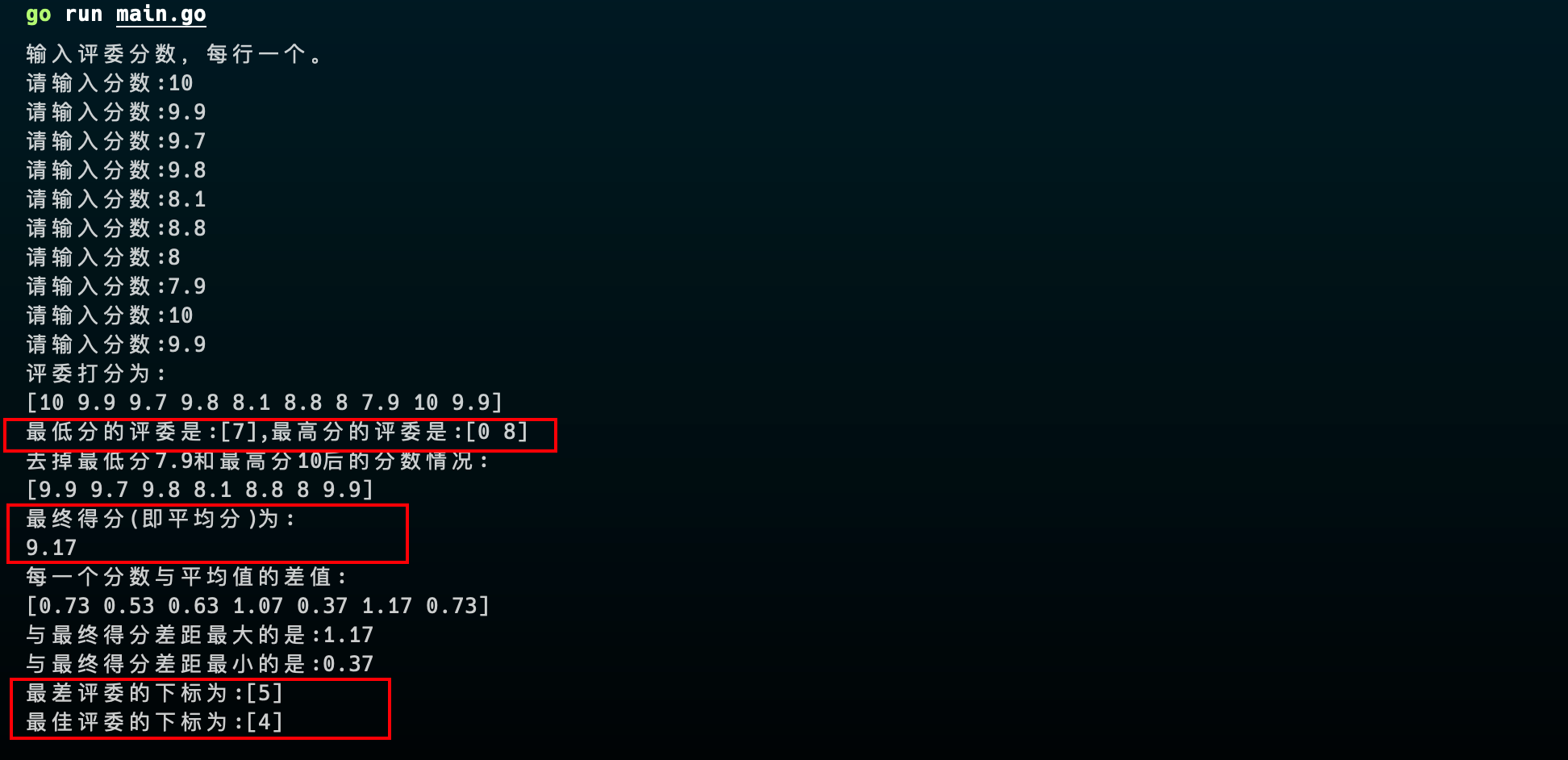
自己写的代码实现的效果

优化建议：

  1. 模块化：将主要功能分解为独立的函数，使代码结构更清晰。现有的Average函数可以进一步拆分为findMinMax和calculateAverage两个函数。
  2. 命名规范：遵循更具描述性的命名规则，如将FindMinMaxIndex改为findMinMaxScoresAndIndices，以明确该函数不仅返回最小值和最大值，还返回对应的评委索引。
  3. 错误处理：在main函数中对findMinMaxScoresAndIndices和findIndices函数的返回值进行错误检查，确保程序在遇到问题时能优雅地处理错误。
  4. 避免重复计算：在findIndices函数中，不需要再次调用FindMinMaxIndex，因为Average函数已经计算了平均分和去掉最高、最低分后的分数数组。可以直接使用这些结果。
  5. 简化findIndices函数：该函数可以简化为遍历新的分数数组，直接计算每个分数与平均分的差值，记录并输出最大差值和最小差值对应的评委索引。
  6. 修正fmt.Printf格式：修复fmt.Printf语句中的一些格式问题，如arr应使用%v而非%.2f来打印整型数组。

优化后的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
package main

import (
	"bufio"
	"errors"
	"fmt"
	"math"
	"os"
	"strconv"
	"strings"
)

// FindMinMaxIndex 函数返回给定浮点数切片中的最小值、最大值及其索引。
// 如果输入切片为空，将返回错误。
func findMinMaxScoresAndIndices(scores []float64) (minScore, maxScore float64, minIndices, maxIndices []int, err error) {
	if len(scores) == 0 {
		return 0, 0, nil, nil, err
	}

	minScore = scores[0]
	maxScore = scores[0]

	for i, v := range scores {
		if v < minScore {
			minScore = v
			minIndices = []int{i}
		} else if v == minScore {
			// 处理相等的情况，将索引添加到 minIndices
			minIndices = append(minIndices, i)
		}
		if v > maxScore {
			maxScore = v
			maxIndices = []int{i}
		} else if v == maxScore {
			// 处理相等的情况，将索引添加到 maxIndices
			maxIndices = append(maxIndices, i)
		}
	}

	return minScore, maxScore, minIndices, maxIndices, nil
}

// 去掉最低分和最高分,算出平均分
func calculateAverage(scores []float64) (average float64, Scores []float64, err error) {
	minScore, maxScore, _, _, err := findMinMaxScoresAndIndices(scores)
	if err != nil {
		return 0, nil, err
	}
	// 标记是否已移除过最低分和最高分
	removedMin, removedMax := false, false
	sum := 0.0
	// 定义切片
	Scores = make([]float64, 0, len(scores)-2)
	for _, v := range scores {
		if !removedMin && v == minScore {
			// 移除一个最低分
			removedMin = true
			continue
		}
		if !removedMax && v == maxScore {
			// 移除一个最高分
			removedMax = true
			continue
		}
		sum += v
		Scores = append(Scores, v)
	}
	average = sum / float64(len(Scores))
	return average, Scores, nil
}

// 计算并返回与平均分最接近和相差最大的评委索引。
func findBestAndWorstJudges(average float64, scores []float64) (bestJudges, worstJudge int, err error) {
	if len(scores) == 0 {
		return 0, 0, errors.New("分数列表不能为空")
	}
	bestDiff, worstDiff := math.MaxFloat64, -math.MaxFloat64
	for i, score := range scores {
		diff := math.Abs(score - average)
		if diff < bestDiff {
			bestDiff = diff
			bestJudges = i
		}
		if diff > worstDiff {
			worstDiff = diff
			worstJudge = i
		}
	}
	return bestJudges, worstJudge, nil
}

func main() {
	reader := bufio.NewReader(os.Stdin)
	scores := make([]float64, 0, 10)
	scoreCount := 0
	fmt.Println("输入评委分数，每行一个。")
	for scoreCount < 10 {
		fmt.Print("请输入分数:")
		input, err := reader.ReadString('\n')
		if err != nil {
			fmt.Println("读取输入时发生错误:", err)
			break
		}
		input = strings.TrimSpace(input)
		if num, err := strconv.ParseFloat(input, 64); err == nil && num >= 0 && num <= 10 {
			scores = append(scores, num)
			scoreCount++
			continue // 正确输入，继续请求下一个分数
		} else {
			fmt.Println("分数必须在0到10之间，请重新输入。")
		}
	}
	if len(scores) > 0 {
		fmt.Printf("评委打分为:\n%v\n", scores)
		average, newScores, err := calculateAverage(scores)
		if err != nil {
			fmt.Println("计算平均分时发生错误:", err)
			return
		}
		minScore, maxScore, minIndices, maxIndices, err := findMinMaxScoresAndIndices(scores)
		if err != nil {
			fmt.Println("请输入分数,分数不能为空")
			return
		}
		fmt.Printf("最低分的评委下标是:%v, 最高分的评委下标是:%v\n", minIndices, maxIndices)
		fmt.Printf("去掉最低分 %v 和最高分 %v 后的分数情况:\n%v\n", minScore, maxScore, newScores)
		fmt.Printf("最终得分(即平均分)为:\n%.2f\n", average)

		bestJudge, worstJudge, err := findBestAndWorstJudges(average, newScores)
		if err != nil {
			fmt.Println("查找最佳和最差评委时发生错误:", err)
			return
		}
		fmt.Printf("与最终得分差距最大的评委下标是：%d（相差%.2f分）\n", worstJudge, math.Abs(newScores[worstJudge]-average))
		fmt.Printf("与最终得分差距最小的评委下标是：%d（相差%.2f分）\n", bestJudge, math.Abs(newScores[bestJudge]-average))
	} else {
		fmt.Println("评委未打分")
	}
}

效果

优化后的效果

code
#Go
Go语言的一些练习题(二)
https://suiyideali.github.io/2024/04/23/Go语言的一些练习题-二/
作者
m0ch4z
发布于
2024年4月23日
更新于
2025年4月2日
许可协议